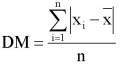MEDIDAS DE DISPERSIÓN

Medidas de dispersión. Parámetros estadísticos que indican como se alejan los datos respecto de la media aritmética. Sirven como indicador de la variabilidad de los datos. Las medidas de dispersión más utilizadas son el rango, la desviación estándar y la varianza.

Rango
Desviación media
Desviación estándar
Error al crear miniatura: Falta archivo
Varianza
Error al crear miniatura: Falta archivo
Coeficiente de Variación
Error al crear miniatura: Falta archivo

Indica la dispersión entre los valores extremos de una variable. se calcula como la diferencia entre el mayor y el menor valor de la variable. Se denota como R.

Para datos ordenados se calcula como:

R = x(n) - x(1)

Donde: x(n): Es el mayor valor de la variable. x(n): Es el menor valor de la variable.

Es la media aritmética de los valores absolutos de las diferencias de cada dato respecto a la media.

Donde:

xi:valores de la variable.

n: número total de datos

La desviación estándar mide el grado de disersión de los datos con respecto a la media, se denota como s para una muestra o como σ para la población. Se define como la raiz cuadrada de la varianza según la expresión:

Obsérvese que el denominador es n - 1, a diferencia de la desviación media donde se divide entre n; también existe la formula de desviación típica donde el denominador es n pero se prefiere n-1.

Mientras menor sea la desviación estándar, los datos son más homogéneos, es decir existe menor dispersión, el incremento de los valores de la desviación estándar indica ina mayor variabilidad de los datos.

Es otro parámetro utilizado para medir la dispersión de los valores de una variable respecto a la media. Corresponde a la media aritmética de los cuadrados de las desviaciones respecto a la media. Su expresión matemática es:

Permite determinar la razón existente entre la desviación estándar (s) y la media. Se denota como CV. El coeficiente de variación permite decidir con mayor claridad sobre la dispersión de los datos.

También puede ser expresado en por ciento.

RAZÓN DE CAMBIO DE UN PROCESO

El concepto de razón de cambio se refiere a la medida en la cual una variable se modifica con relación a otra. Se trata de la magnitud que compara dos variables a partir de sus unidades de cambio. En caso de que las variables no estén relacionadas, tendrán una razón de cambio igual a cero.

Razón de cambio (de una variable respecto a otra) es la magnitud del cambio de una variable por unidad de cambio de la otra. (También se le llama tasa de cambio.) Si las variables no tienen ninguna dependencia la tasa de cambio es cero.

En general, en una relación funcional y=f(x)$y=f(x)$, la razón de cambio de la variable dependiente y$y$ respecto a la independiente x$x$ se calcula mediante un proceso de límite --de la razón [f(x+t)−f(x)]/t$[f(x+t)-f(x)]/t$, denominada cociente diferencial.

En sentido estricto entonces, la razón de cambio es el límite del cociente diferencial cuando t$t$tiende a cero. De esta manera, la razón de cambio es la interpretación fundamental de la derivada de una función.

En la función lineal f(x)=mx+b$f(x)=mx+b$, no es necesario tomar el límite pues  f(x+t)−f(x)=mx+mt+b−mx−b=mt$f(x+t)-f(x)=mx+mt+b-mx-b=mt$ y la t se cancela en la razón [f(x+t)−f(x)]/t$[f(x+t)-f(x)]/t$ sin necesidad de pasar al límite.

Nótese que m$m$ es la pendiente de la recta f(x)=mx+b$f(x)=mx+b$. Y es la razón de cambio de la altura y$y$ (variable dependiente) respecto a la x$x$ (variable independiente. Viéndolo gráficamente, es el cambio en la altura y$y$ por unidad de cambio (aumento) en la x$x$.

En matemáticas escolares la razón de cambio más usada es la velocidad: v=d/t$v=d/t$ (distancia recorrida por unidad de tiempo). La velocidad es, de hecho, la razón de cambio ejemplar o prototipo. Por analogía, se le llama "velocidad" a una razón de cambio cualquiera. Por ejemplo, en problemas de proporción inversa.

1. 1. Razón de cambio  Se conoce como razón de cambio a la medida en que una variable cambia con respecto a otra, como por ejemplo la velocidad, la cual es una razón de cambio del espacio con respecto al tiempo: lim(Dx/Dt, t tiende a cero)
2. 2. Diferencial  Un diferencial se define como un infinitesimal, que es una diferencia entre dos puntos de una misma variable, pero que dicha diferencia es extremadamente pequeña, tanto que tiende a ser cero, se acerca mucho al cero, pero no llega a ser 0: Da tiende a 0.
3. 3. Aplicaciones  Las aplicaciones son varias, para la razón de cambio, su principal uso es la minimización o maximización de funciones. Son usados en economía (para minimizar costos, maximizar calidad, etc.),física (evaluar la máxima velocidad de un cuerpo, por ejemplo), geometría (minimizar la cantidad de material para construir un cilindro, por ejemplo), etc.
4. 4. Aplicaciones  Son muchas las aplicaciones de la razón de cambio. Para las estimaciones de los errores puede ser usado en los cálculos por medio de métodos numéricos. Los diferenciales son usados principalmente para cálculos más excatos en una suma, pues el integral se define como la sumatoria de diferenciales, en sí el integral es una suma. La función más conocida para la estimación de error es la "función error" (erf(x)), el cual se defiene como: erf(x)=int(f(x)dx,0,x)/raiz(2*pi)
5. 5. Ejemplos de una razon de cambio  Comenzando por la Razón Instantánea de Cambio de una función cuya variable independiente es el tiempo t. suponiendo que Q es una cantidad que varía con respecto del tiempo t, escribiendo Q=f(t), siendo el valor de Q en el instante t. Por ejemplo El tamaño de una población (peces, ratas, personas, bacterias,…) La cantidad de dinero en una cuenta en un banco El volumen de un globo mientras se infla La distancia t recorrida en un viaje después del comienzo de un viaje El cambio en Q desde el tiempo t hasta el tiempo t+"t, es el incremento

USOS DE LA TRIGONOMETRÍA

La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. Deriva de los términos griegos τριγωνοϛ trigōnos 'triángulo' y μετρον metron 'medida'.¹

En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Posee numerosas aplicaciones, entre las que se encuentran: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas globales de navegación por satélites.

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Para definir las razones trigonométricas del ángulo: ${\displaystyle \alpha }$, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

• La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.

• El cateto opuesto (a) es el lado opuesto al ángulo ${\displaystyle \alpha }$.

• El cateto adyacente (b) es el lado adyacente al ángulo ${\displaystyle \alpha }$.

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

${\displaystyle \operatorname {sen} \alpha ={\frac {\color {ForestGreen}{\textrm {opuesto}}}{\color {Red}{\textrm {hipotenusa}}}}={\frac {a}{h}}}$

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo ${\displaystyle \alpha }$ , en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

${\displaystyle \cos \alpha ={\frac {\color {Blue}{\textrm {adyacente}}}{\color {Red}{\textrm {hipotenusa}}}}={\frac {b}{h}}}$

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

${\displaystyle \tan \alpha ={\frac {\color {ForestGreen}{\textrm {opuesto}}}{\color {Blue}{\textrm {adyacente}}}}={\frac {a}{b}}}$

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

${\displaystyle \cot \alpha ={\frac {\color {Blue}{\textrm {adyacente}}}{\color {ForestGreen}{\textrm {opuesto}}}}={\frac {b}{a}}}$

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

${\displaystyle \sec \alpha ={\frac {\color {Red}{\textrm {hipotenusa}}}{\color {Blue}{\textrm {adyacente}}}}={\frac {h}{b}}}$

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

${\displaystyle \csc \alpha ={\frac {\color {Red}{\textrm {hipotenusa}}}{\color {ForestGreen}{\textrm {opuesto}}}}={\frac {h}{a}}}$